What is Integration Testing? A Complete Guide to Integration Testing

Integration testing is a key level of testing to find defects where software components and system interface together. Testing functions in isolation is important, but falls short of testing software behavior in ways it will actually be used in conjunction with other items.

In software testing, a productive strategy is to look for defects and failures where they may be most likely to occur. One thing we have learned over the years, supported by credible research, is that software failures are much more likely to manifest where interactions occur.

However, once we start to design and perform tests based on integration, the complexity that arises from many points of integration can increase the number of possible tests to massive numbers.

Furthermore, integration testing can be seen in many ways which also increases the challenge. Some may see integration testing as only part of continuous integration (CI) in a build process, others may perform integration at a component level as various software components are created or changed, while others may have a wider scope of integration testing in a system testing, acceptance testing, or a systems-of-systems context.

In this article, we explore the various levels of integration testing, as well as the difference between integration and interoperability testing. You will also learn how to design tests that can deal with the high levels of complexity often seen in highly integrated system architectures.

Interoperability Testing vs Integration Testing

When comparing these two terms, we need to understand that integration testing is a level of testing, while interoperability testing is a type of testing. This is important to understand because both integration and interoperability testing are typically needed to fully validate how software behaves when a transfer of data or control occurs. In addition, types of testing can be performed at multiple levels of testing as seen in Figure 1.

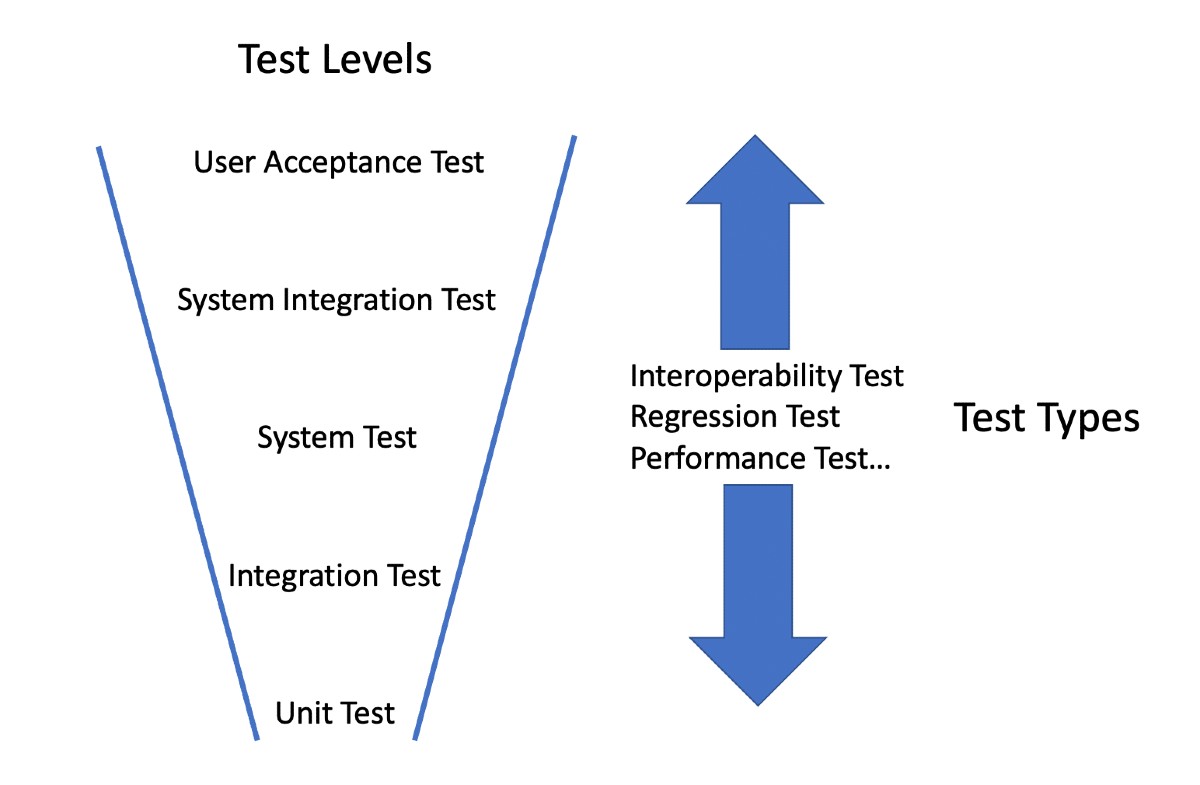
Figure 1 – Levels and Types of Testing

As an example, integration testing can show what happens when data is sent from one component to another. Interoperability testing can show what happens when someone uses the data that has been exchanged to perform some type of further action.

Integration testing can validate that two or more systems or components can exchange data or control correctly. There are two major levels of integration testing, component integration testing (sometimes called low-level integration testing) as seen in Figure 2 and system integration testing (sometimes called high-level integration testing) seen in Figure 3.

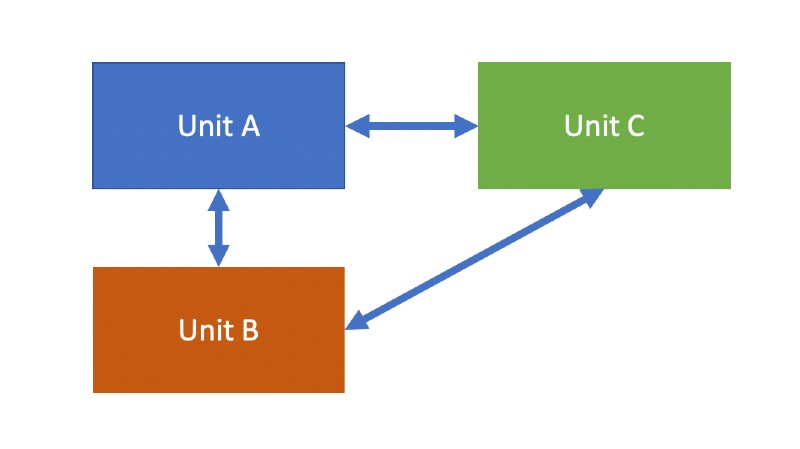
Figure 2 – Component Integration Testing

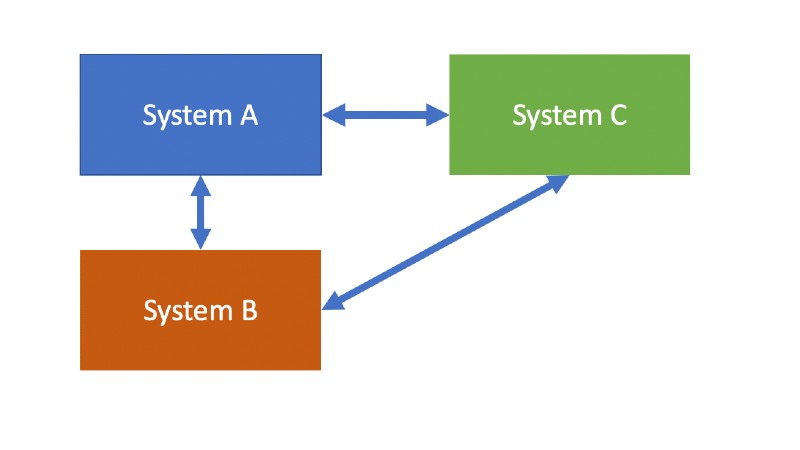
Figure 3 – System Integration Testing

The main difference is the level at which integration is tested. As we will see later in this article, the complexity increases greatly at the system integration level.

However, interoperability testing is needed to show that the true user need can be achieved in an operational context. Both integration and interoperability testing are typically needed to verify and validate how well software components and systems work together.

Why do we need integration testing?

Research in software testing interactions goes back at least 35 years when some of the first papers were published on the topic of using combinatorial techniques for software testing. At least thirty-eight papers and presentations have been published since that date.

Early methods were based in Latin squares which is another name for orthogonal arrays. The point of the combinatorial techniques for integration testing is to deal with extremely high numbers of possible combinations of test conditions.

This problem is often seen when integration is present between related functions, components, and/or systems, and when the combined test conditions would yield far too many possible test cases to realistically implement and perform.

An example of this need for integration testing is in the domain of medical devices. Obviously, this is a domain where safety criticality is a very high concern and complexity can be very high due to the high number of configuration parameters.

In a research paper published in 2001 by Delores Wallace and Richard Kuhn of the National Institute of Standards and Technology¹, over 15 years of medical device recall report data was analyzed. One of the most interesting findings was that “… of the 109 reports that are detailed, 98% showed that the problem could have been detected by testing the device with all pairs of parameter settings.”

This is a significant finding because it suggests that if we could at least test all the pairs of related conditions, we could test where many of the integration defects reside. If testing only pairs of conditions leaves more to be desired, “n-wise” testing can test 3-wise, 4-wise and higher.

This is not an isolated finding and it gives support to the idea of testing related functions, such as in the case of integration testing, with techniques such as pairwise testing to help manage the very high number of possible interactions that could possibly be tested.

NIST has a free tool called ACTS (Automated Combinatorial Testing for Software) that generates test cases based on n-wise testing.

Other domains which also have the need for integration testing which reach almost impossible levels of test condition combinations include automotive (especially with emerging autonomous vehicle technologies), avionics, financial and the Internet of Things (IoT).

While combinatorial testing is helpful and promising, it does have limitations in that it can be somewhat random how the condition combinations are derived. In fact, some important test conditions may be missed altogether. This leaves the need to include other techniques which we explore in this article.

What are the different types of integration testing?

There are some key ways to achieve integration in computing systems. Some are more reliable than others. In Figure 4 we see how these levels of integration can be achieved in a pyramid-like approach.

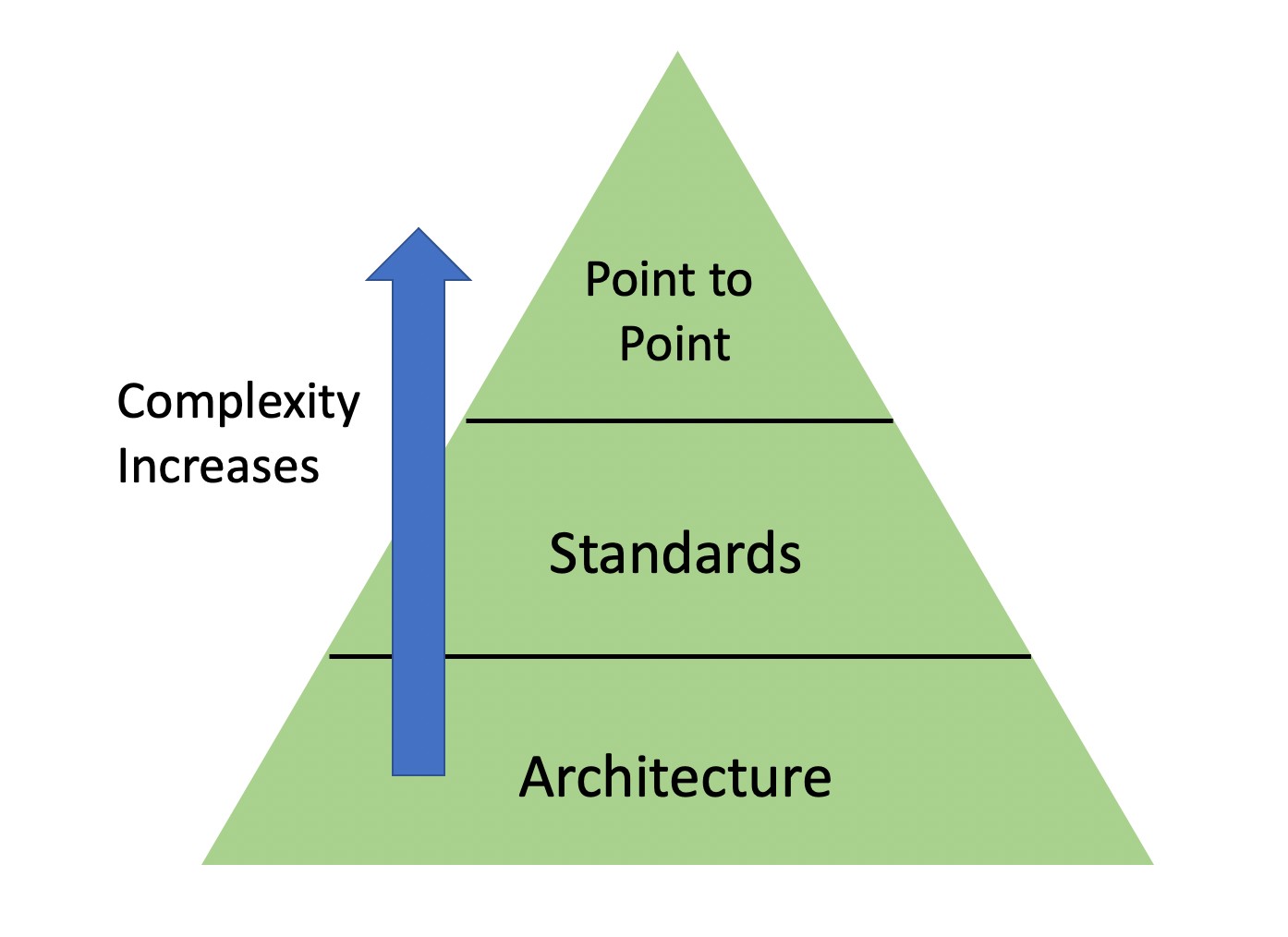
Figure 4 – Integration Approaches

Point-to-point

This is where integration points are defined one at a time. If there are a significant number of interfaces, the integration can become messy and confusing. Complexity levels can skyrocket, which also increase the likelihood of defects

Testing point-to-point integration can be very tedious, with a potentially large number of tests. This is a context where combinatorial methods, such as pairwise testing, are helpful to reduce the number of tests.

Standards-based

In this approach, the idea is that if you follow a particular standard followed by others, you will achieve integration. This is better than point-to-point integration in terms of complexity, but it relies upon all parties following the standard. This may not be a valid assumption. Integration testing is based on following the standard, but can also test in a negative way to see where the standard may not be followed.

Architecture-based

In this approach, integration occurs when all the components are in the same architectural domain. An example of this is a service-oriented architecture. To be in the architecture, components must follow the same rules for integration.

Therefore, if a service or other component complies with the architecture, integration is assumed. Integration testing is designed and performed at an architectural level. This can be very helpful to also validate interoperability within the architecture.

Using a test plan for integration testing

The process proposed below is based on the concept of test planning. While test planning may be out of style in some organizations, there is still a strong need for such planning especially where integration is concerned.

One of the defining features of integration testing is that of coordination of effort between all parties impacted. For example, in testing the integration between systems that may span organizations, you may need to ensure the people on both sides of the interfaces are available and able to verify the test results.

How to do integration testing?

The process described here is somewhat sequential, but is also iterative and evolving since new information will likely emerge throughout the life cycle of an application.

1. Assess Applications, Risk and Environments – This involves taking an inventory of applications and functions to be tested (including COTS applications), inventorying interfaces, defining application profiles and listing known application compatibilities and incompatibilities, and performing a risk assessment.
2. Test Planning – In this activity, the scope of testing is defined, as well as responsibilities and schedule. Also, test and operational environments are defined and the needed test tools are acquired and implemented. It is in this activity that testing efforts are coordinated with affected parties.
3. Test Design – This is the activity where tests are designed and implemented, including prioritizing tests based on risk and identifying workflow scenarios that cover integration points.
4. Test Implementation – This is where you create test cases and procedures, along with the test data to support the tests.
5. Test Execution – In this activity you conduct and evaluate tests along with reporting incidents as failures are seen.
6. Test Reporting – This is where test findings are reported, including test status reports and the final test report.
7. Follow-up Testing – This is where follow-up testing such as confirmation testing and regression testing are performed as changes are made to the components and systems.

The Role of API Integration Testing

One of the primary ways integration is achieved today is through Application Programming Interfaces (APIs). While many people mainly think of APIs in a web-based or mobile application context, APIs are also used to interface with operating systems and other system components and applications.

API testing may appear to be straightforward, but it can be rather challenging due to inadequate documentation of the interface. In addition, too often people test only that data can traverse the API, failing to test APIs in negative ways by trying to pass invalid data through the interface, or testing data that has been encoded in a way the receiver doesn’t expect.

The Role of Integration Testing Tools

Tools such as Postman and SoapUI can provide a helpful framework for defining and performing API tests, but there is still a need to manage and report API tests. This is where test management tools such as PractiTest are needed.

Integration Testing Example with PractiTest

PractiTest provides a quick and easy way to organize tests by test level, test phase and other categories, including custom categories.

In Figure 5 we see an integration test to validate purchasing a product from an e-commerce web site. The integration is implemented by the use of APIs and spans several functions such as authentication, product selection, shopping cart, checkout, payment authorization, and purchase confirmation.

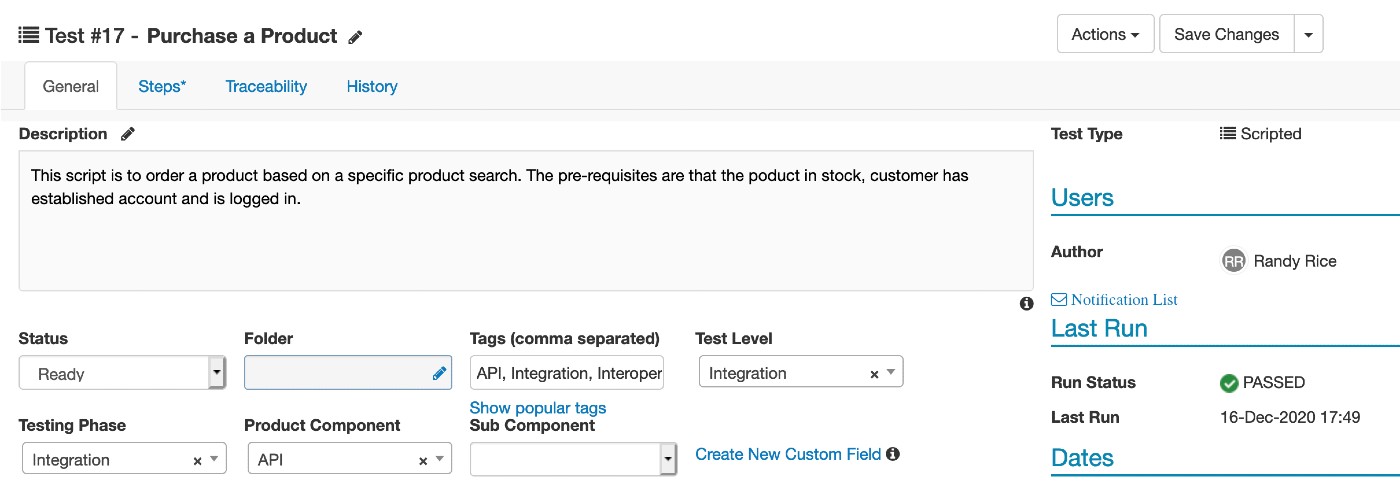
Figure 5 – Integration Test in PractiTest

More Integration Testing Examples With Interoperability Testing

Many of my clients have faced a common problem, which is the ability to test integration and interoperability in a “system of systems” context. In this context, various systems must interact together correctly to accomplish the desired outcomes.

The problem arises when point-to-point integration is the primary means of integration. In reality, systems integrate at the component level. So, it is actually components that are passing data and control between each other, spanning systems. An example of this is shown in Figure 6.

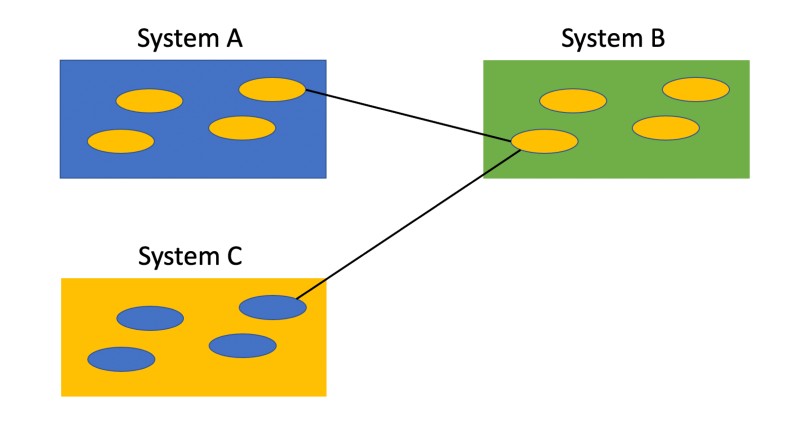
Figure 6 – “Point to Point” Integration Between Systems

As an example, suppose one component in one system (A) is changed which impacts the data sent to another system (B). System B may in turn call a function in another system (C). Perhaps these interfaces are all known to a tester so they perform the tests and see that integration and interoperability is achieved correctly.

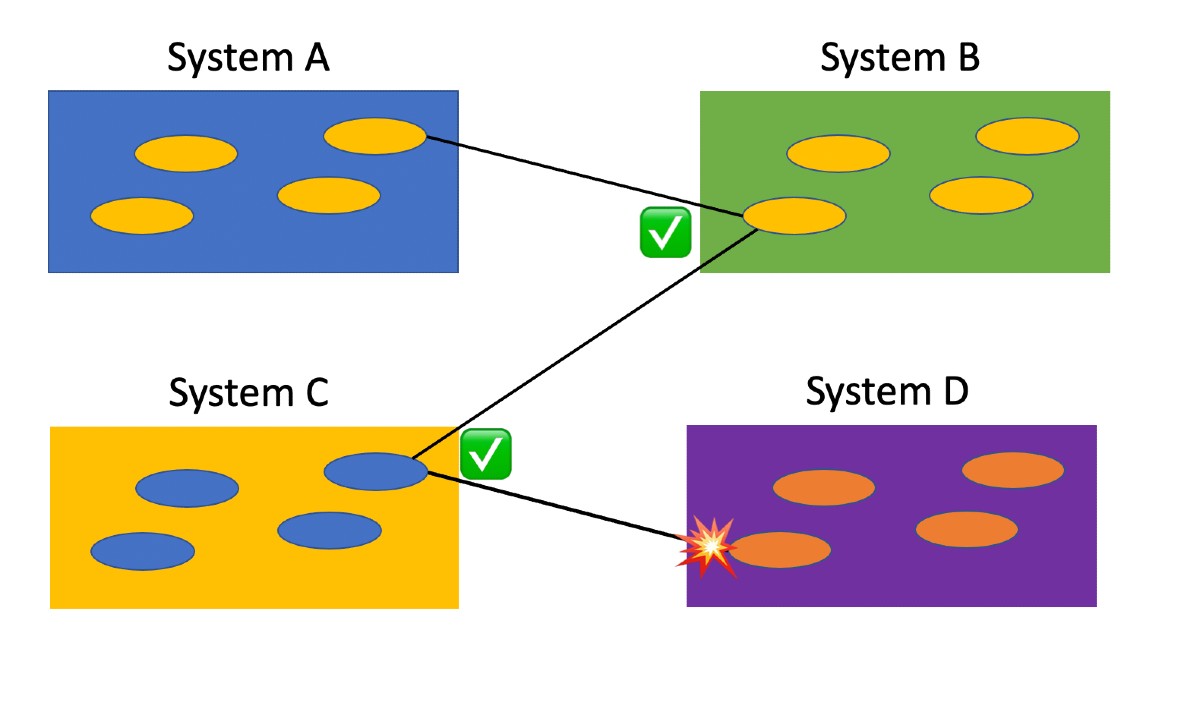
Figure 7 – “Downstream” Integration Failure

However, let’s also consider the situation where the above scenario also triggers a function in a fourth system (D) (Figure 7). At this point, a failure occurs. The integration and interoperability wasn’t tested because no one considered system D was even part of the picture. Much of this is due to a lack of documentation or knowledge about where integration occurs in this point-to-point approach.

These “downstream” failures can be quite frustrating because it seems at times like you can never test enough.

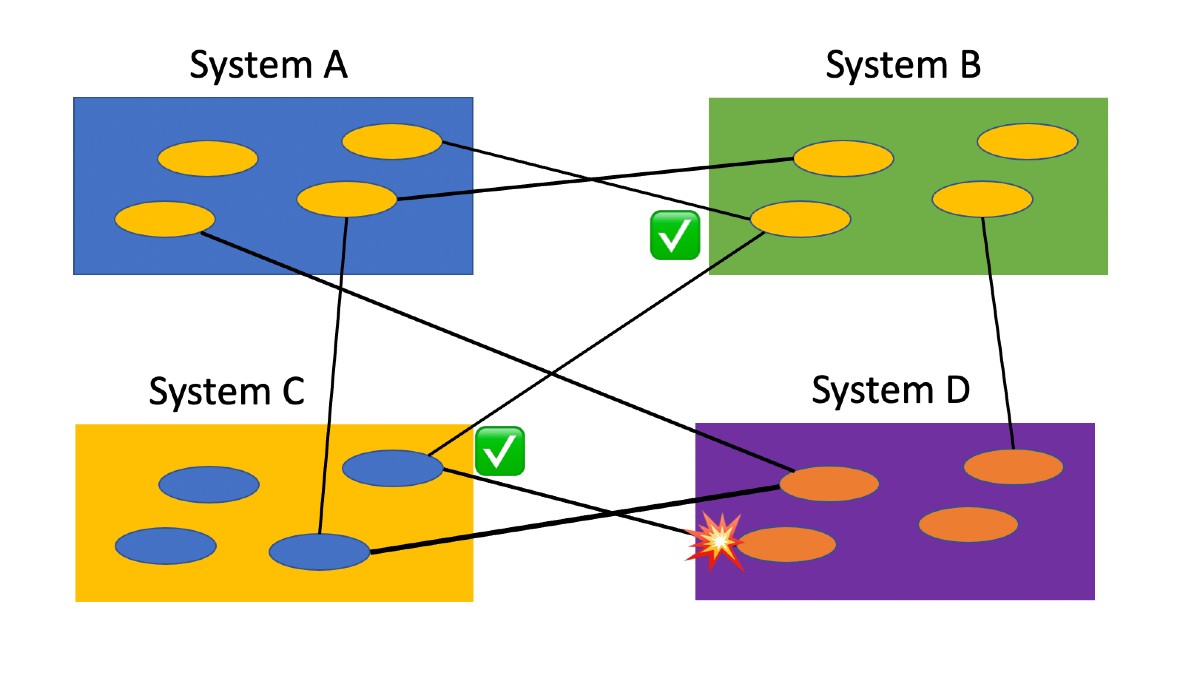
Figure 8 – The Spider Web Emerges

In this example, the integration takes on a spider web appearance (Figure 8), except spider webs have more order to them! The ability to adequately test integration and interoperability depend on the ability to know where the integration exists. However, this knowledge is often missing or limited which leads to untested interfaces and missed defects.

One proven way I deal with this problem is to focus testing on workflow scenarios (Figure 9). In testing the workflows, you automatically cover the integration points and also validate interoperability.

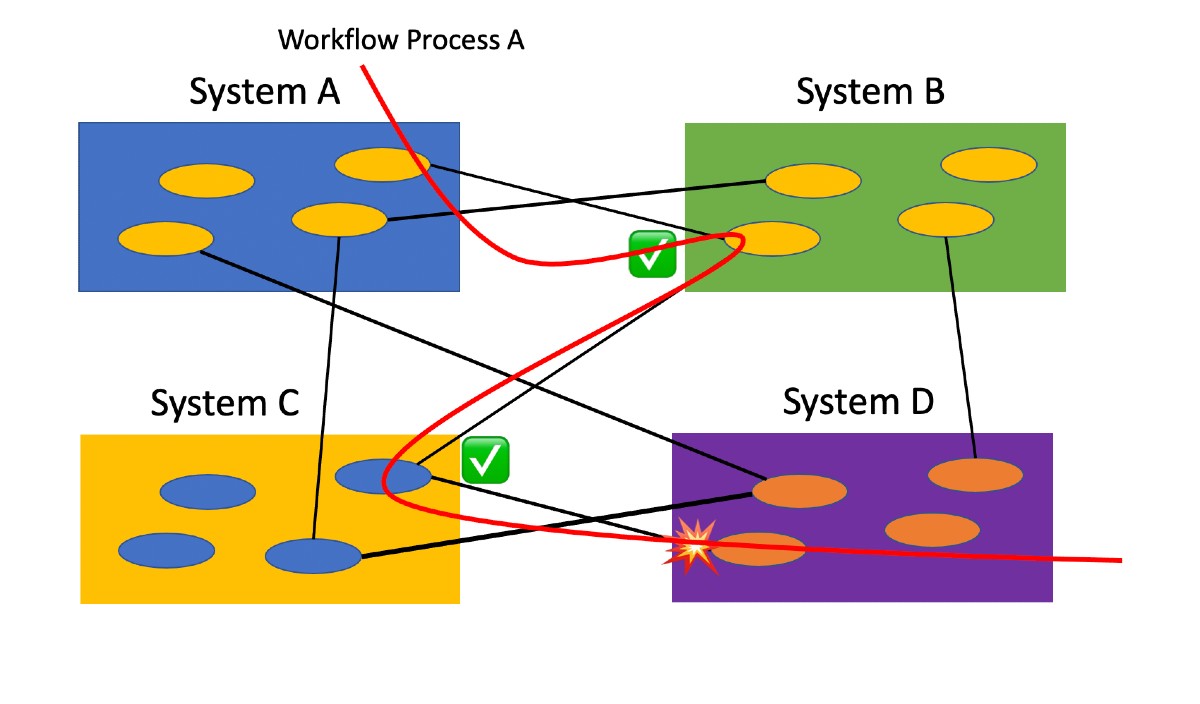
Figure 9 – Focusing testing on workflow scenarios

In essence, this is end-to-end testing that spans systems. This approach can be applied within a single system as well.

You also gain an economy of testing by taking the scenario view. At the component level, there are many conditions to consider which lead to higher numbers of tests. At the scenario level, it might be possible to test the same coverage of interfaces with a fraction of the test cases needed at the detailed level.

Conclusion

Integration testing can be quite challenging due to the high number of possible integration paths that arise from point-to-point integration approaches which tend to be complex and fragile. However, by applying combinatorial approaches and workflow scenarios, it may be possible to lessen the risk of integration failures.

Randall W. Rice, CTAL

Randall W. Rice is a leading author, speaker, consultant and practitioner in the field of software testing and software quality, with over 40 years of experience in building and testing software projects in a variety of domains, including defense, medical, financial and insurance.

You can read more at his website.